Big O notation with C++

Preamble

Summary about Big O notation may be found here…

Headlines

Fibonacci

Euclid

Quick sort

Heap & priority queue

Fibonacci

Fibonacci sequence here can be implemented through 3 methods: recursive, iterative, or Binet formula here…
class Fibonacci {
	static long _COST;
public:
	enum Method { Recursive, Iterative, Binet };
	const static double Golden_number;
	const double result;
	long cost;
	Fibonacci(long = 0L, Method method = Method::Recursive);
private:
	long _recursive(long) const;
	long _iterative(long) const;
	long _binet(long) const;
};
Recursive method
long Fibonacci::_recursive(long n) const {
	assert(n >= 0L);
	if (n == 0L) return 0L;
	if (n == 1L) return 1L;
	_COST++;
	return _recursive(n - 1L) + _recursive(n - 2L);
}
#include <iostream>

#include <sys/timeb.h> // "more < /usr/include/sys/timeb.h" with UNIX

#include "Fibonacci.h"

int main(int argc, char** argv) {
    timeb start, end;
    ::ftime(&start);
    std::cout << "start: " << start.time << "." << start.millitm << "\n";
    Fibonacci fibonacci(5L); // Default method is "Fibonacci::Method::Recursive"...
    ::ftime(&end);
    std::cout << "end: " << end.time << "." << end.millitm << "\n";
    std::cout << "result: " << fibonacci.result << "\n"; // '5'
    std::cout << "cost: " << fibonacci.cost << "\n"; // '7'

    return 0;
}
Complexity (a.k.a. “cost”) can be measured by the number of calls to the Fibonacci::_recursive function minus the number of calls to Fibonacci(0) and Fibonacci(1), which are constant values.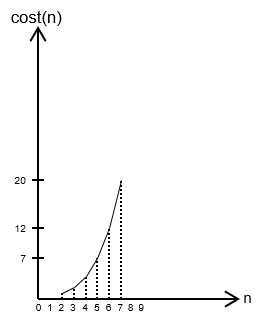

The line chart embodies a fast-growing function and illustrates complexity of Fibonacci recursive method. Complexity class is O(2ⁿ) and characterizes time-greedy algorithms. Other key complexity classes in this area are O(n²) - quadratic, O(n^c) - polynomial, O(cⁿ) with c > 1 - exponential, and O(n!) - factorial.

Iterative method

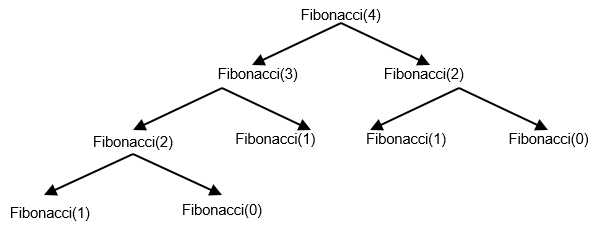
Pitfall of the recursive method is the useless computation of intermediate values of Fibonacci. For example, Fibonacci(4) generates two computations of Fibonacci(2) while one is enough.

So, the iterative method just implements the trick: intermediate values of Fibonacci are computed once.
long Fibonacci::_iterative(long n) const {
	assert(n >= 0L);
	if (n == 0L) return 0L;
	if (n == 1L) return 1L;
	long u = 1L, v = 0L, u0, v0;
	for (long i = 2L; i <= n; i++) {
		_COST++;
		u0 = u;
		v0 = v;
		u = u0 + v0;
		v = u0;
	}
	return u;
}
#include <iostream>

#include <sys/timeb.h> // "more < /usr/include/sys/timeb.h" with UNIX

#include "Fibonacci.h"

int main(int argc, char** argv) {
	timeb start, end;
	::ftime(&start);
	std::cout << "start: " << start.time << "." << start.millitm << "\n";
	Fibonacci fibonacci(5L, Fibonacci::Method::Iterative); // Default method is "Fibonacci::Method::Recursive"...
	::ftime(&end);
	std::cout << "end: " << end.time << "." << end.millitm << "\n";
	std::cout << "result: " << fibonacci.result << "\n"; // '5'
	std::cout << "cost: " << fibonacci.cost << "\n"; // '4'

	return 0;
}
Complexity of Fibonacci::_iterative function is O(n) - linear.

Binet method

A key point behind the Binet method is the fact that complexity of the computation is hidden by complexity of the ::pow function coming from the C programming language. Note that Golden_number variable may be computed once and for all (at compilation time if desired by means of constexpr); it does impact complexity of the computation.
long Fibonacci::_binet(long n) const {
    assert(n >= 0L);
    return long((::pow(Golden_number, double(n)) - ::pow((1. - Golden_number), double(n))) / ::sqrt(5.));
}
Application(s)

Fibonacci.Cpp.zip

Euclid

Euclid algorithm is described here…
class Euclid {
private:
    long _a, _b, _result;
    inline long _compute(long, long) const;
public:
    inline Euclid(long, long);
    inline long result() const;
};

long Euclid::_compute(long a, long b) const {
    if (b == 0L) return a;
    return _compute(b, a % b);
}

Euclid::Euclid(long a, long b) : _a(a), _b(b), _result(0L) {
    assert(_a >= 0L && _b > 0L);
    _result = _compute(_a, _b);
}

long Euclid::result() const {
    return _result;
}
#include <iostream>

#include "Euclid.h"

int main() {
    Euclid e(18L, 12L);
    std::cout << "Euclid: " << e.result() << std::endl;
    
    return 0;
}
In analyzing the _compute function, one observe that a variable acts as a constant in recursive calls while it is the contrary for b variable. In fact, complexity of the _compute function is O(n*log(n)) - logarithmic linear, but code does not make it actually explicit.

Exercise

Introduce an “artificial” variable that measures cost, i.e., increment this variable at each recursive call of the _compute function.

Empirically check that cost is closed to b*log(b) by means of the ::log function coming from the C programming language.

Application(s)

Euclid.Cpp.zip

Quick sort

Quick sort algorithm is described here… Its complexity is n*log(n) while “slow” sort complexity is O(n²) (see i-based loop and jbased -loop imbrication within Sort_illustration::_sort function below).

class Sort_illustration {
    int* _representation;
    int _size;
    void _sort(int, int, int&); // Slow
    int _split(int, int, int&);
    void _quick_sort(int, int, int&); // Quick
public:
    enum Speed { Slow, Quick };
    Sort_illustration(int);
    ~Sort_illustration();
    int sort(Speed = Slow);
};

#include <algorithm> // 'std::swap', etc.
#include <cassert>
#include <cstdlib> // 'std::srand', etc.
#include <ctime>

#include "Sort_illustration.h"

void Sort_illustration::_sort(int left, int right, int& cost) {
    assert(left < right);
    for (int i = left; i < right; i++) {
        for (int j = i + 1; j <= right; j++) {
            cost++;
            if (_representation[i] > _representation[j]) std::swap(_representation[i], _representation[j]);
        }
    }
}

int Sort_illustration::_split(int left, int right, int& cost) {
    int pivot = left;
    int value = _representation[left];
    for (int i = left + 1; i <= right; i++) {
        cost++;
        if (_representation[i] < value) {
            pivot++;
            std::swap(_representation[pivot], _representation[i]);
        }
    }
    std::swap(_representation[left], _representation[pivot]);
    return pivot;
}

void Sort_illustration::_quick_sort(int left, int right, int& cost) {
    if (right - left <= 0) return;
    int pivot = _split(left, right, cost);
    _quick_sort(left, pivot - 1, cost);
    _quick_sort(pivot + 1, right, cost);
}

Sort_illustration::Sort_illustration(int size) : _size(size) {
    assert(_size > 0);
    _representation = new int[_size];
    time_t t;
    std::srand(std::time(&t));
    for (int i = 0; i < _size; i++) _representation[i] = std::rand();
}

Sort_illustration::~Sort_illustration() {
    delete[] _representation;
}

int Sort_illustration::sort(Speed speed) {
    int cost = 0;
    switch (speed) {
        case Slow: _sort(0, _size - 1, cost);
            break;
        case Quick: _quick_sort(0, _size - 1, cost);
            break;
        default:;
    }
    return cost;
}

#include <algorithm> // 'std::sort', etc.
#include <cmath> // '::log'
#include <iostream>
#include <numeric> // 'std::accumulate', etc.
#include <vector>

#include "Sort_illustration.h"

int main(int argc, char** argv) {
    int n = 10000;
    Sort_illustration si(n);
    std::cout << si.sort(Sort_illustration::Quick) << '\n';
    std::cout << "n*log(n): " << n * ::log(n) << std::endl;

    short tab[] = {13, 7, 6, 4, 12, 11, 8, 3};
    std::vector<short> vector(tab, tab + 8);
    for (int i = 0; i < vector.size(); i++) std::cout << "-" << vector[i];
    std::cout << std::endl;
    std::sort(vector.begin(), vector.end());
    for (int i = 0; i < vector.size(); i++) std::cout << "-" << vector[i];
    std::cout << std::endl;

    return 0;
}

Exercise

Check that computation time of std::sort function coming from the C++ standard library is close to computation time of homemade quick sort. This especially has to occur when the number of to-be-sorted values is “big”.

Tools

Randomization: std::srand(unsigned int) and std::rand() in #include <cstdlib>
Time measurement: time_t and tm types in #include <ctime> or timeb type in #include <sys/timeb.h> (location: more < /usr/[local/]include/sys/timeb.h with UNIX)

Application(s)

Sort_illustration.Cpp.zip

Heap & priority queue

Priority queues (a.k.a. heaps) are backed by arrays whose management is that of a AVL (“height-balanced”) tree here… Note that a AVL tree is a rooted (one and only one root) binary search tree.

Tree on the left-hand side is not “height-balanced” because at level 2 (root is level 0), one node has two child nodes while its sister node has no child at all; difference is 2. Difference must be less than or equal to 1 to satisfy the “height-balanced” property. Tree on the right-hand side satisfies the “height-balanced” property for any node.

The added value of priority queues is fact that the most prioritized element is the root of the tree, namely, the element at index 0 in the backed array. To that extent, complexity for getting/searching this most prioritized element is O(1) - constant.

Rule(s)

left(x) is located in the array at the (2 * i) + 1 position where i is the position of x

right(x) is located in the array at the (2 * i) + 2 position

So, in the figure, the root, 13, is located at 0 while 12 is located at 2 * 0 + 1 = 1, etc.
-13-12-11-8-6-7-4-3 // Backed array...
Insertion
Insertion leads to maintain “a queue of priorities” so that, later on, getting/searching prioritized elements relies on getting/searching elements in a “height-balanced” binary rooted tree. Complexity of operations on priorities queues is O(log(n)) - logarithmic.
template<typename T, int default_capacity = 10> class Heap {
private:
	T* _content; // Or 'T _content[];'
	int _n;
public:
	const int capacity;
	Heap(int capacity = default_capacity) : capacity(capacity) {
		assert(capacity > 0);
		_content = new T[capacity];
		_n = 0;
	}
	~Heap() {
		delete[] _content;
	}
	void insert(const T& t) {
		assert(_n < capacity);
		_content[_n++] = t;
		int i = _n - 1;
		for (int j = i / 2; i > 0 && _content[j] < _content[i]; j /= 2) {
			std::swap(_content[i], _content[j]);
			i = j;
		}
	}
	int size() const {
		return _n;
	}
	void sort(T result[]) const {
		assert(result);
		for (int i = 0; i < _n; i++) result[i] = _content[i];
		assert(_n > 1);
		for (int i = _n - 1; i > 0; i--) {
			std::swap(result[i], result[0]);
			int max;
			for (int j = 0; 2 * j + 1 < i; j = max) {
				if (2 * j + 2 == i) max = 2 * j + 1;
				else max = result[2 * j + 1] > result[2 * j + 2] ? 2 * j + 1 : 2 * j + 2;
				if (result[max] > result[j]) std::swap(result[max], result[j]);
			}
		}
	}
};
Example (insertion of 9)
-13-12-11-8-6-7-4-3-9
-13-12-11-8-9-7-4-3-6
Sort (a.k.a. “heap sort”)

Example

Support in C++
C++ provides the two std::make_heap and std::sort_heap functions (#include <algorithm>) to immediately have the possibility of dealing with heaps/priority queues.

Example (creation)
short my_array[] = { 3, 4, 6, 7, 8, 11, 12, 13 };
std::vector<short> my_vector(my_array, my_array + 8);
for (int i = 0; i < my_vector.size(); i++) std::cout << "-" << my_vector[i];
/* Display: '-3 - 4 - 6 - 7 - 8 - 11 - 12 - 13' */
std::cout << std::endl;
std::make_heap(my_vector.begin(), my_vector.end());
for (int i = 0; i < my_vector.size(); i++) std::cout << "-" << my_vector[i];
/* Display: '- 13 - 8 - 12 - 7 - 3 - 11 - 6 - 4' */
std::cout << std::endl;
Example (sort)
std::sort_heap(my_vector.begin(), my_vector.end());
for (int i = 0; i < my_vector.size(); i++) std::cout << "-" << my_vector[i];
/* Display: '-3 - 4 - 6 - 7 - 8 - 11 - 12 - 13' */
std::cout << std::endl;
-13-8-12-7-3-11-6-4
Since the backed array slightly differs from the homemade version, explanations may be found here…

Application(s)

Heap.Cpp.zip

Big O notation with C++

Recursive method

Iterative method

Binet method

Application(s)

Exercise

Application(s)

Exercise

Tools

Application(s)

Rule(s)

Insertion

Example (insertion of `9`)

Sort (a.k.a. “heap sort”)

Example

Support in C++

Example (creation)

Example (sort)

Application(s)

Big O notation with C++

Recursive method

Iterative method

Binet method

Application(s)

Exercise

Application(s)

Exercise

Tools

Application(s)

Rule(s)

Insertion

Example (insertion of 9)

Sort (a.k.a. “heap sort”)

Example

Support in C++

Example (creation)

Example (sort)

Application(s)

Example (insertion of `9`)